convergencia | Profesor Delta

Definición de convergencia de sucesiones

junio 1, 2010

La definición de convergencia permite formalizar toda la idea intuitiva que tenemos de límite de números, para así poder utilizar y manipular límites (álgebra de límites)

¿Cuál es la idea intuitiva que tenemos de límite?

Bueno, sabemos (o intuimos) que el límite de $\frac{1}{n}$ converge a cero cuando n tiende a infinito. Pero sabemos que $\frac{1}{n}$ es distinto de cero para todo n mayor que uno. ¿Entonces? Ocurre que la sucesión $\frac{1}{n}$ SE ACERCA LO MAS QUE PUEDE A 0, aunque increíblemente nunca llegue a tocarlo. Luego, el concepto de límite se refiere principalmente al concepto de que tan cerca se encontrara la sucesión a un punto de convergencia (llamado límite).

El primer concepto a considerar es que la distancia entre 2 números reales a y b se denota $|a-b|$ , que es el valor absoluto de la diferencia. Así la distancia entre un punto $x_n$ de la sucesión y su límite L (si es que existe) es $|x_n-L|$ .

Probablemente, esta distancia nunca llegue a ser cero (como en la sucesión 1/n), pero ciertamente los puntos deberían ir acercándose a su límite.

La definición formal de convergencia de la sucesión $x_n$ a un punto L es

Para todo $\epsilon >0$ , existe un $\exists n_{\epsilon} \in \mathbb{N}$ , tal que para todo $n > n_{\epsilon} ,\ |x_n -L|< \epsilon$

O como se suele encontrar en los textos de cálculo, en un lenguaje formal:

$\forall \epsilon >0 ,\ \exists n_{\epsilon} \in \mathbb{N} :\ \forall n>n_{\epsilon} ,\ |x_n - L|< \epsilon$

¿Qué quiere decir realmente?

Dice: Para cualquier distancia que queramos ver del limite ( $\epsilon$ ), siempre podemos encontrar una posición en la sucesión ( $n_{\epsilon}$ ), de tal forma que todos los términos de la sucesión a partir de esta posición $n_{\epsilon}$ , caen dentro de esta vecindad del límite. Trata de asimilar esta descripción en palabras y entenderlo con la definición formal.

Ahora vamos a mostrar como funciona con la sucesión $\frac{1}{n}$ .

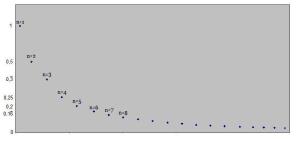
Grafiquemos la sucesión $x_n=\frac{1}{n}$ .

En esta imagen, los puntos corresponden a los términos de la sucesión, y la altura de estos puntos representa el valor de este término. Así, para n=1, la sucesión toma el valor 1, para n=2, el valor 0.5, para n=5, $x_5$ =0.2.

Podemos ver en la imagen que la sucesión se acerca gradualmente al valor cero (y como sabemos, nunca lo alcanza)

¿Cómo funciona la definición formal acá?

Supongamos que un compañero te pregunta ¿Desde que punto la sucesión $x_n$ no se aleja a más de 0,5 del valor cero? Al ver el dibujo, notamos que desde el término $x_2$ la sucesión no sube de 0,5.

¿Y desde qué término la sucesión no se aleja a lo más de 0,2 de cero? Viendo nuevamente el dibujo, podemos notar que desde el término $x_6$ en adelante no se supera la barrera impuesta (línea roja). También puedes decir que a partir del término 8; no tiene que ser necesariamente el término exacto (la definición formal no lo pide)

Y así hacia el infinito. Es decir, si tu compañero te pregunta ¿A partir de qué término no me alejo una distancia $\epsilon$ (con $\epsilon$ quiero decir cualquier distancia >0) del cero? tu siempre vas a poder encontrar una posición n a partir del cual la sucesión no se aleje. En términos matemáticos.

para todo $\epsilon >0$ , existe un $n_e$ tal que para todo $n > n_{\epsilon}$ , $x_n <\epsilon$ .

Esta definición, y la anterior discusión, no obliga a la sucesión a alcanzar su límite, pero sí la obliga a siempre acercarse tanto como queramos (o tanto como quiera tu compañero).

Con el dibujo queda claro, pero demostremos formalmente (o como debería ser en la prueba) que $x_n=1/n$ converge a 0.

¿Qué pasa si queremos que todos los puntos de la sucesión estén a una distancia menor o igual a 1? Bueno como todos los términos de la sucesión son menores o iguales que 1, después del término unésimo se cumple.

¿Qué pasa si queremos que todos los puntos de la sucesión estén a una distancia menor o igual que 1/10. Bueno notamos que para n=10, los términos son menores a 1/10. ( $x_{10}=\frac{1}{10}$ )

¿Y si queremos que no se alejen a lo mas 1/100? Entonces notamos que los términos no se alejan de esa distancia después del punto n=100. ( $x_{100}=\frac{1}{100}$ ).

Ahora te diste cuenta que para cualquier distancia que nos demos (digamos $\epsilon$ ) el punto necesario para cumplir la definición es darse el $n=\frac{1}{\epsilon}$ o mayor).

Pero la fórmula que les dí no está de todo correcta, pues para $\epsilon=0.013$ , $n=\frac{1000}{13}=76,9230769$ , que no es natural. Pero no nos importa, pues no queremos un número exacto tal que todos las términos de la sucesión no se alejen, lo que queremos es uno que nos asegure que pase lo que queremos, así en vez de decir $76,9230769$ podemos decir simplemente $n=77$ , y cumplimos nuestro objetivo. Así, mejorando nuestro razonamiento

Para $\epsilon$ cualquiera, $n_{\epsilon}=[\frac{1}{\epsilon}]$ . (Función parte entera).

on este ejemplo también notamos que el n elegido depende de $\epsilon$ , por eso en la definición de límite se suele colocar $n_{\epsilon}$ .

Hagamos la demostración como deberías colocarla en la prueba (lo que esta en paréntesis son indicaciones que no debes escribir).

Problema: demuestre que la sucesión $x_n=\frac{1}{n}$ converge a cero

Dem:

Sea $\epsilon >0$ (nos damos una distancia cualquiera, como la que te pregunta tu compañero).

Queremos encontrar un $n_{\epsilon}$ tal que para todo $n>n_{\epsilon}$ se tenga

$|x_n-0|< \epsilon$ .

trabajando esta expresión.

$|x_n-0|=|\frac{1}{n}|<\epsilon = \frac{1}{n}<\epsilon$ .

(Equivalentemente, el problema se reduce a encontrar un $n_{\epsilon}$ que cumpla que para todo $n>n_e$ se tenga $\frac{1}{n}< \epsilon$ , lo cual se tiene si n cumple $\frac{1}{\epsilon} <n$ ).

eligiendo $n_{\epsilon}=[\frac{1}{e}]$ se tiene lo pedido.

$\square$

Problema: demuestre que la sucesión constante $a_n=c$ converge a c.

Dem:

Sea $\epsilon >0$ .

$|a_n-c|=|c-c|=0<\epsilon$ (¡¡la distancia entre la sucesión y su limite siempre es cero!!!)

Tomando n=1, se tiene lo pedido (o n igual cualquier cosa, total siempre estamos a una distancia menor que $\epsilon$ )

$\square$

En este caso particular, la sucesión si alcanza su límite.

Ahora demostremos la siguiente propiedad, que nos permitirá justificar el álgebra de límites.

Propiedad: Sean $a_n$ y $b_n$ dos sucesiones tales que $a_n\xrightarrow[n\rightarrow{}\infty]\,{a}$ y $b_n\xrightarrow[n\rightarrow{}\infty]\,{b}$ . Entonces $a_n+b_n\xrightarrow[n\rightarrow{}\infty]\,{a+b}$ .

Demostración:

Sea $\epsilon>0$ (la distancia fija que siempre nos debemos dar)

$|a_n+b_n-(a+b)|=|(a_n-a)+(b_n-b)|<|a_n-a|+|bn-b|$

Como $a_n$ converge a $a$ , tenemos que para cualquier distancia que queramos, existe un $n^{*}$ tal que para $n>n^*$ , $|a_n-a|$ es menor que dicha distancia. Luego si la distancia que queremos es $\frac{\epsilon}{2}$ , existe un $n_1$ tal que para $n > n_1$ , $|a_n-a| < \frac{\epsilon}{2}$ .

Análogamente, para la sucesión $b_n$ , existe un $n_2$ (no necesariamente igual a $n_1$ , pues $b_n$ es un sucesión no necesariamente igual a $a_n$ ) tal que para $n > n_2 ,\ |b_n-b|<\frac{\epsilon}{2}$ .

Entonces para $n_3=max(n_1,n_2)$

$|a_n-a|< \frac{\epsilon}{2}$ y $|b_n-b|<\frac{\epsilon}{2}$ .

De este modo , para todo $n>n_3$ .

$|a_n-a|+|b_n-b| < \frac{\epsilon}{2}+\frac{\epsilon}{2} =\epsilon$

Reordenando lo logrado, para todo $n>n_3$ .

$|a_n+b_n-(a+b)| =|a_n-a+b_n-b| <|a_n-a|+|b_n-b| < \epsilon$ .

$\square$

Nota que la convergencia de $a_n$ nos asegura la existencia de $n_1$ , y la convergencia de $b_n$ asegura la de $n_2$ . Por lo tanto $n_3=\max(n_1,n_2)$ existe.